Visualization and Summary Statistics
UCLA Soc 114
Review of last class
Say this code in English:
- Store the vector
c(1,2,3)in the objectnumbers - Use the
length()function to get the length ofnumbers
Learning goals for today
- Reason about distributions
- and visualize with
ggplot()
- and visualize with
- Understand summary statistics
- and construct with
summarize()
- and construct with
- Write clean code with the pipe
|>
How to visualize?
How might we visualize the U.S. income distribution?
Here are some data:
# A tibble: 1,000 × 2
id hhincome
<dbl> <dbl>
1 1 19170.
2 2 124474.
3 3 25114.
# ℹ 997 more rowsVisualize with a histogram
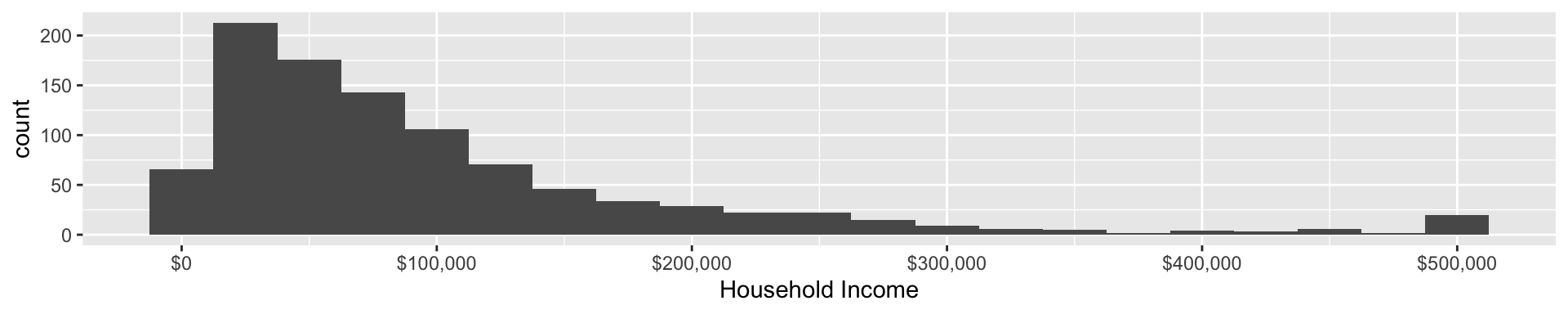
- Bins of $25,000
- In each bin, count number of people
Learning a new function: ggplot
Two arguments get us started:
dataargument contains datamappingargument maps data to plot elements
Within mapping,
aes()defines the aesthetics of the plot- i.e. which variable goes along x-axis
Adding a layer: geom_histogram()
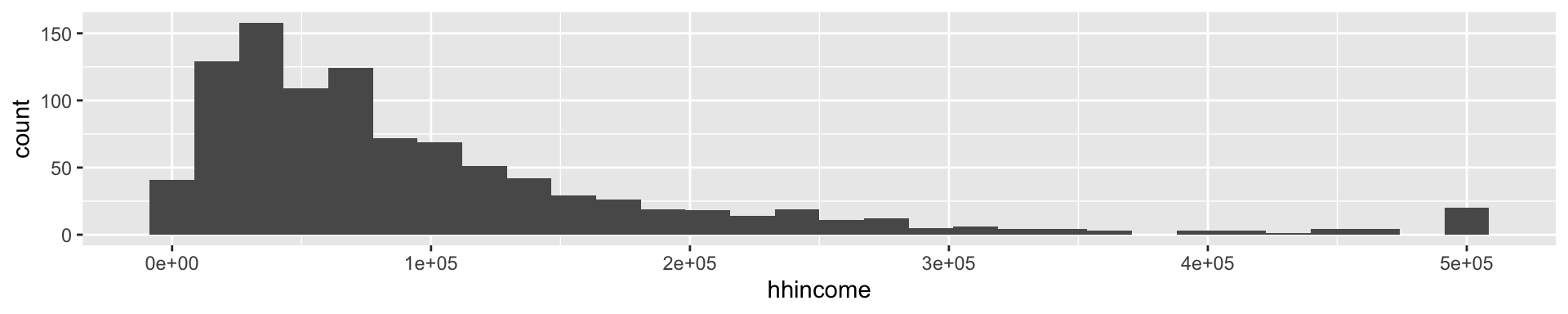
- The
+indicates that a new layer is coming geom_histogram()is the new layer- Inherits the
dataandmappingof the plot
Update axis titles
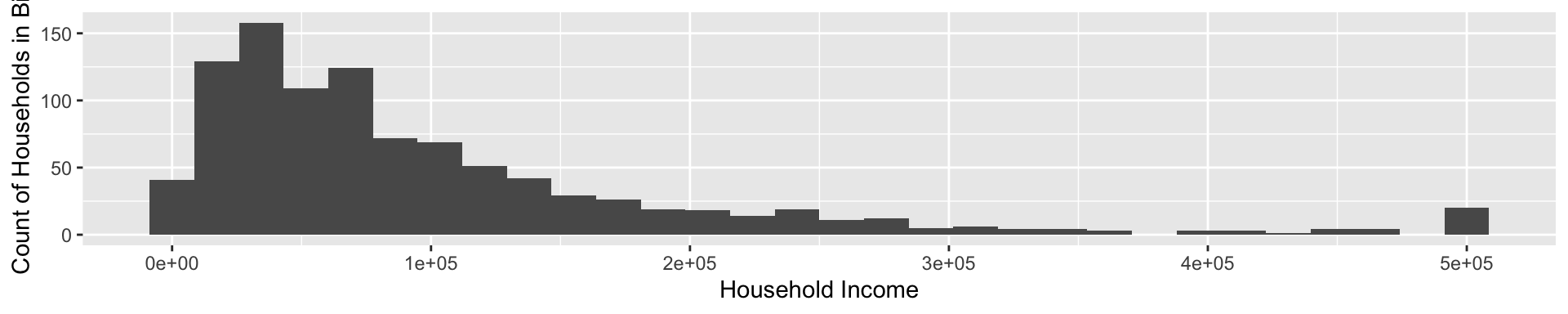
Learning goals for today
- Reason about distributions
- and visualize with
ggplot()
- and visualize with
- Understand summary statistics
- and construct with
summarize()
- and construct with
- Write clean code with the pipe
|>
Imagine 3 income distributions
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
Normative question: Which one is better?
Summary statistic
A summary statistic aggregates a distribution to one number
For example, the mean \[\text{mean}(\vec{x}) = \frac{x_1 + x_2 +\cdots}{n}\]
Summary statistic: Mean
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
| Mean | $73k | $58k | $58k |
By the mean, Distribution 1 seems the best.
Summary statistic: Median
- Sort households by income.
- Find where 50% of households have higher incomes
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
Summary statistic: Median
- Sort households by income.
- Find where 50% of households have higher incomes
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
| Median | $60k | $65k | $60k |
By the median, Distribution 2 seems the best.
Aside: Percentiles generalize the median
The median is the value in the middle
- 50% of people have lower values
- Also called the 50th percentile
Generalizes to other percentiles
- 10th percentile: Value such that 10% are lower
- 90th percentile: Value such that 90% are lower
These summarize the bottom and top of a distribution.
Summary statistic: Minimum
Find the lowest value.
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
Summary statistic: Minimum
Find the lowest value.
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
| Minimum | $10k | $40k | $50k |
By the minimum, Distribution 3 seems the best.
Which summary statistic to choose?
Minimum? Median? Mean?
| Household | Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|
| 1 | $10k | $40k | $50k |
| 2 | $60k | $65k | $60k |
| 3 | $150k | $70k | $65k |
Choosing a summary statistic
Which summary to choose is not an empirical question.
- Depends on what aspect of the distribution matters to you
The value of a chosen summary statistic is empirical.
- Data can tell us a value for the mean, the median, the minimum, etc.
The summarize() function
The summarize() function aggregates data to summaries.
- Input is a dataset with \(n\) rows
- Output is a summary with 1 row
The summarize() function
# A tibble: 1,000 × 2
id hhincome
<dbl> <dbl>
1 1 19170.
2 2 124474.
3 3 25114.
# ℹ 997 more rowsThe summarize() function
# A tibble: 1 × 1
estimated_mean
<dbl>
1 100899..datais input dataestimated_meanis a variable in output datamean(hhincome)is the mean household income
The summarize() function: Several summaries
Learning goals for today
- Reason about distributions
- and visualize with
ggplot()
- and visualize with
- Understand summary statistics
- and construct with
summarize()
- and construct with
- Write clean code with the pipe
|>
Piping code with |>
The pipe |> passes x as the first argument to the length() function.
Piping code with |>
Stylistically helpful
- Data is a different kind of argument
- Pipes will help us in the future
Learning goals for today
- Reason about distributions
- and visualize with
ggplot()
- and visualize with
- Understand summary statistics
- and construct with
summarize()
- and construct with
- Write clean code with the pipe
|>