Confidence Intervals
UCLA Soc 114
Concepts for today
Statistical concepts
- Sampling distribution
- Standard error
- Confidence interval
- Bootstrap
Coding concepts
- Writing a custom function
- Writing a for loop
Example: Mean salary of MLB players
Load data:
# A tibble: 944 × 3
player team salary
<chr> <chr> <dbl>
1 Bumgarner, Madison Arizona 21882892
2 Marte, Ketel Arizona 11600000
3 Ahmed, Nick Arizona 10375000
# ℹ 941 more rowsExample: Mean salary of MLB players
True mean in population of all players
Estimate from a sample
Draw a sample of 10 players.
Estimate from a sample
Take the mean among sampled players.
Many times
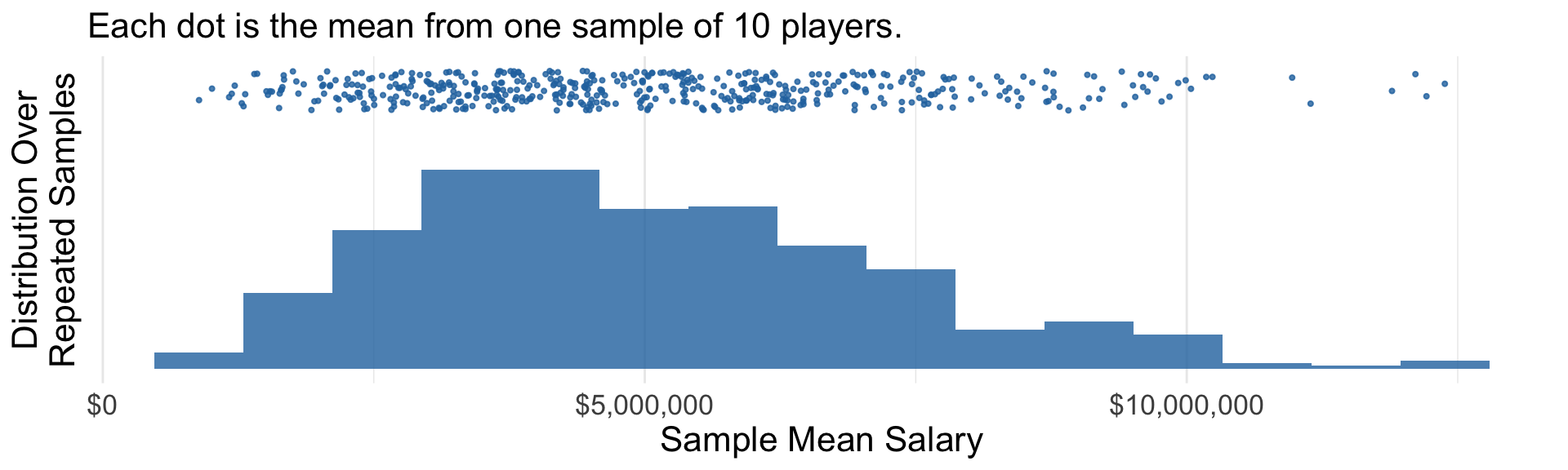
If you are following, these are in many_samples.csv.
Because each sample produces a different estimate, there is a distribution of different estimates across repeated samples.
Can you propose a summary statistic for this distribution?
Mean of the distribution
Also called the expected value.
# A tibble: 1 × 1
estimator_mean
<dbl>
1 5036657.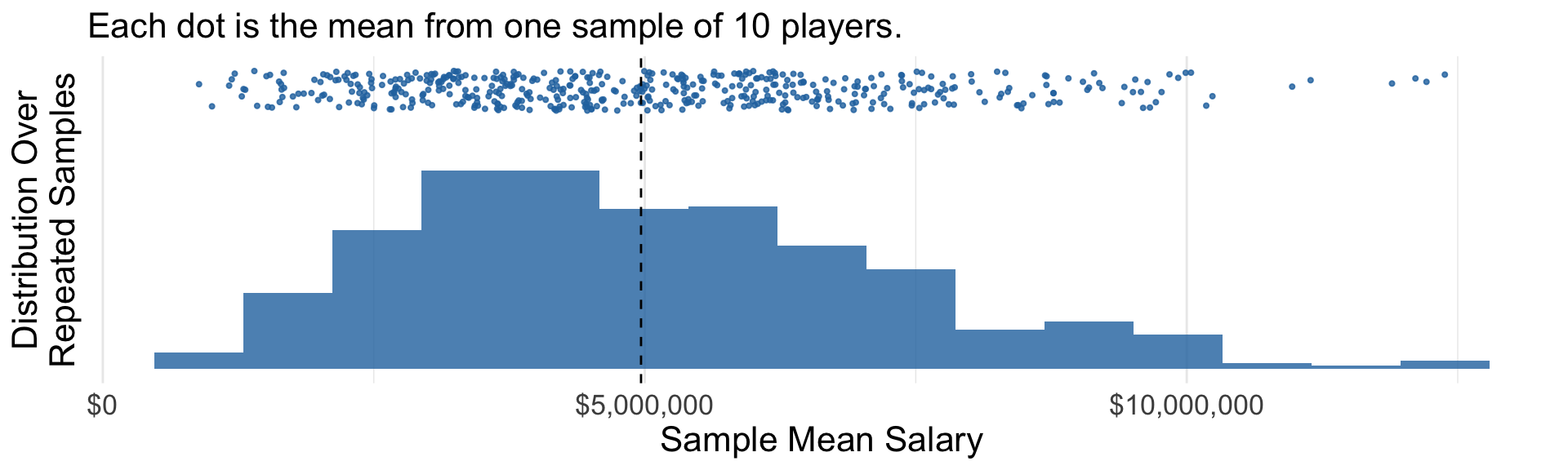
(In practice, the mean of the distribution is unknown)
Standard Error
A measure of dispersion for the distribution of sample mean estimates.
# A tibble: 1 × 1
standard_error
<dbl>
1 2210213.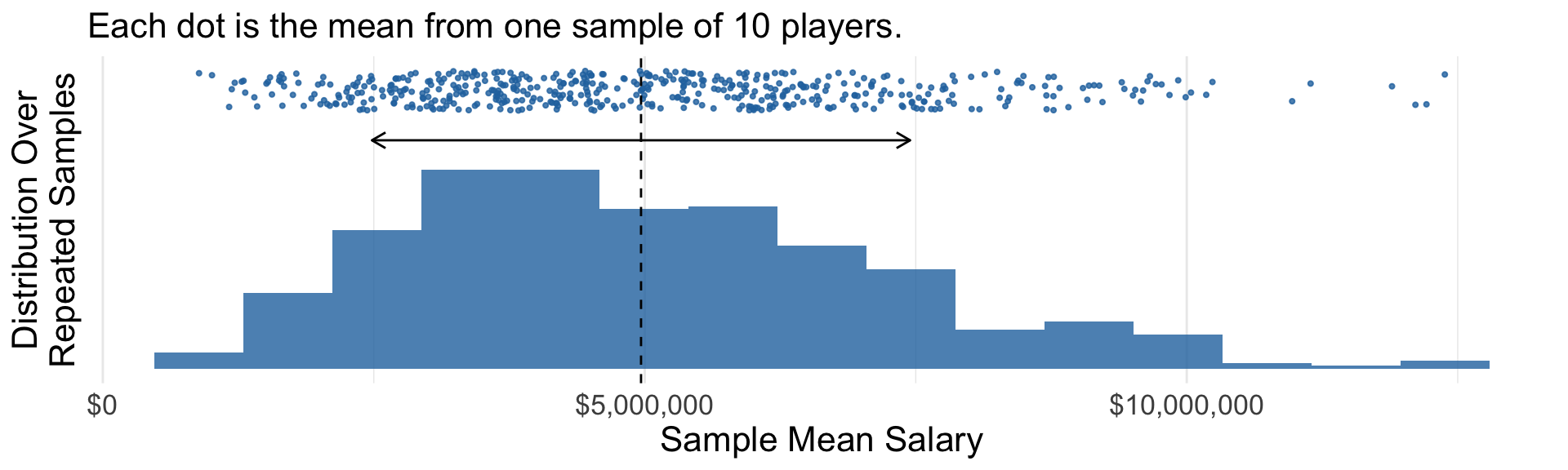
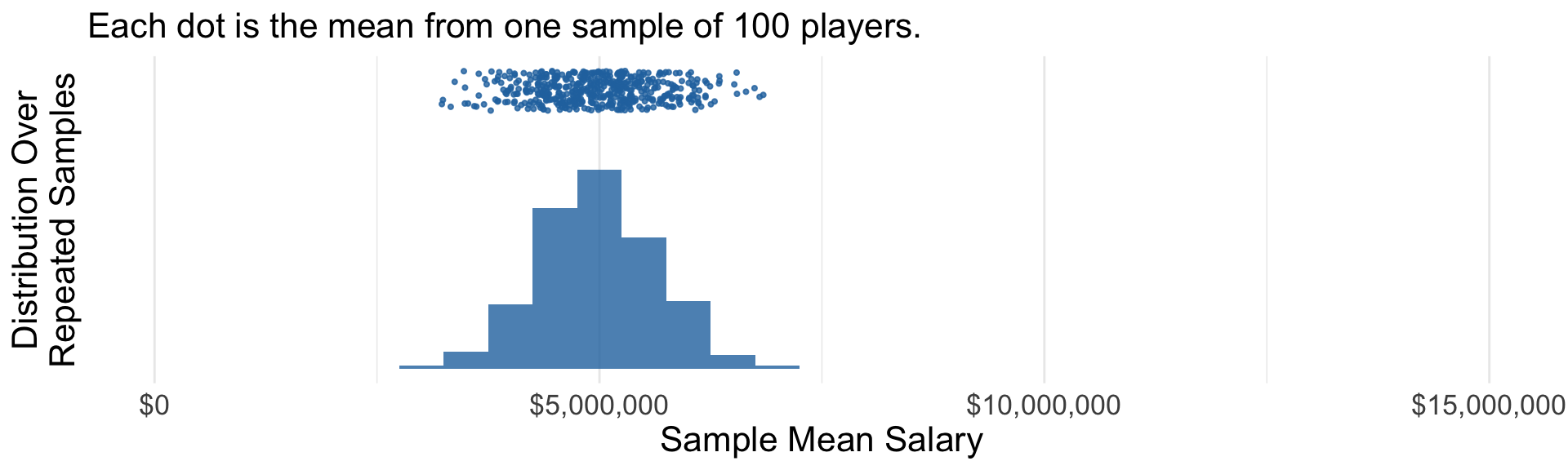
As the sample size grows
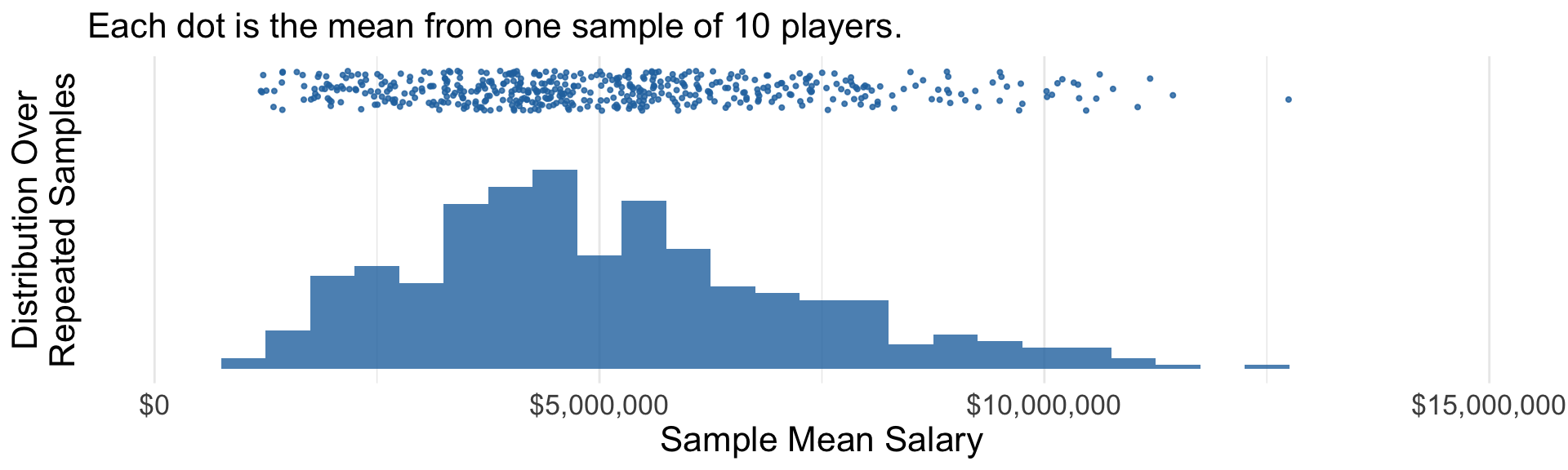
As the sample size grows
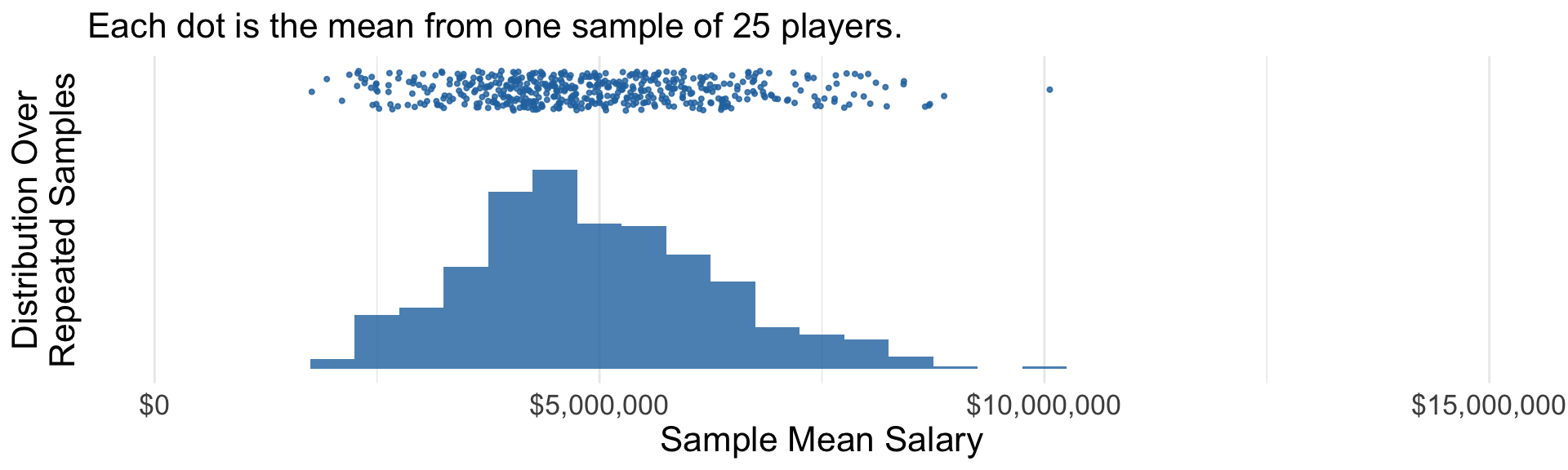
As the sample size grows
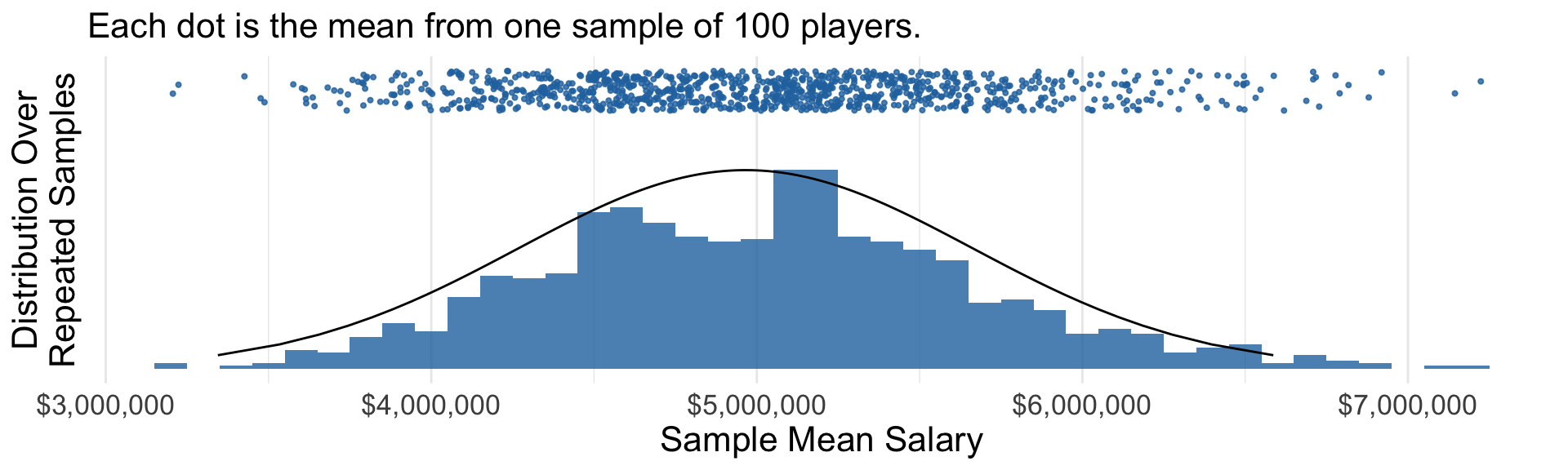
Asymptotic Normality
- As the sample size gets large (asymptotic)
- This becomes a Normal distribution
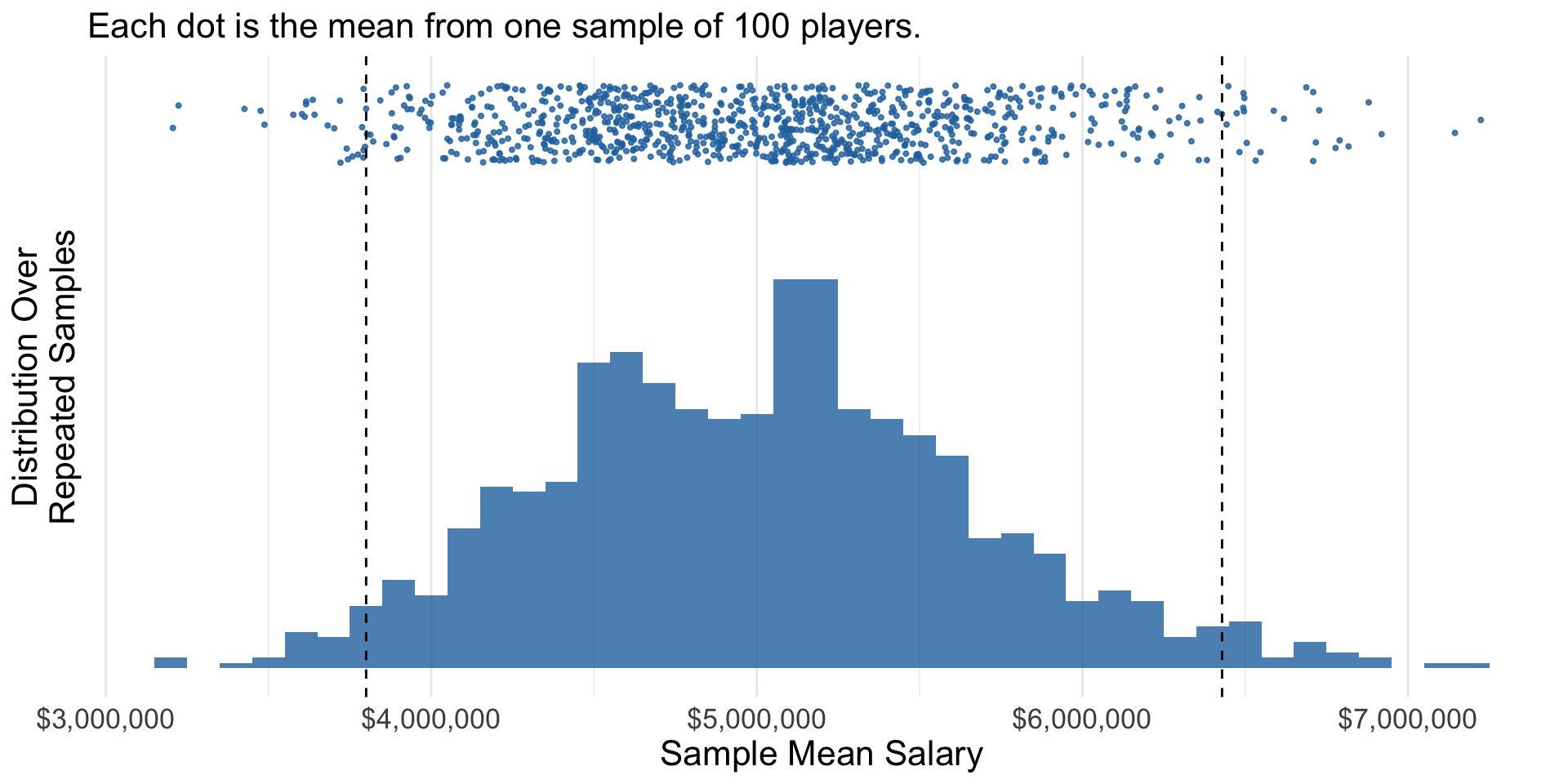
Middle 95% sampling interval
We might want to summarize:
- The mean of the estimator
- A range containing the middle 95% of sample estimates
Why is that hard to do with one actual sample?
Confidence interval via the bootstrap
What we want:
- We would want many samples:
sample_1,sample_2,sample_3,… - We estimate with each
- We summarize the middle 95%
Confidence interval via the bootstrap
What we can do:
- We get only one
sample- So we simulate hypothetical
sample_sim_1,sample_sim_2,…
- So we simulate hypothetical
- We estimate with each
- We summarize the middle 95%
How to generate bootstrap samples
Start with your one sample.
How to generate bootstrap samples: Example
Here is a sample of 3 players:
How to generate bootstrap samples: Example
Here is a bootstrap sample of those 3 players.
How to generate bootstrap samples: Example
Here is a bootstrap sample of those 3 players.
How to generate bootstrap samples: Example
Here is a bootstrap sample of those 3 players.
How to generate bootstrap samples: Example
Here is a bootstrap sample of those 3 players.
Coding concepts
We will analyze hundreds of bootstrap samples.
We need two coding concepts.
- How to write an
estimatorfunction - How to write a
forloop
How to write an estimator function
A function (like mean) takes an input and returns an output. You can write your own.
The function takes data and returns an estimate.
How to write a for loop
Useful for tasks you will repeat.
First, initialize a vector to hold results.
The rep function repeates the value NA 3 times.
Analyze 500 bootstrap samples
Initialize a vector to hold the result.
Analyze 500 bootstrap samples
Write a for loop that will repeat 500 times.
Bootstrap results
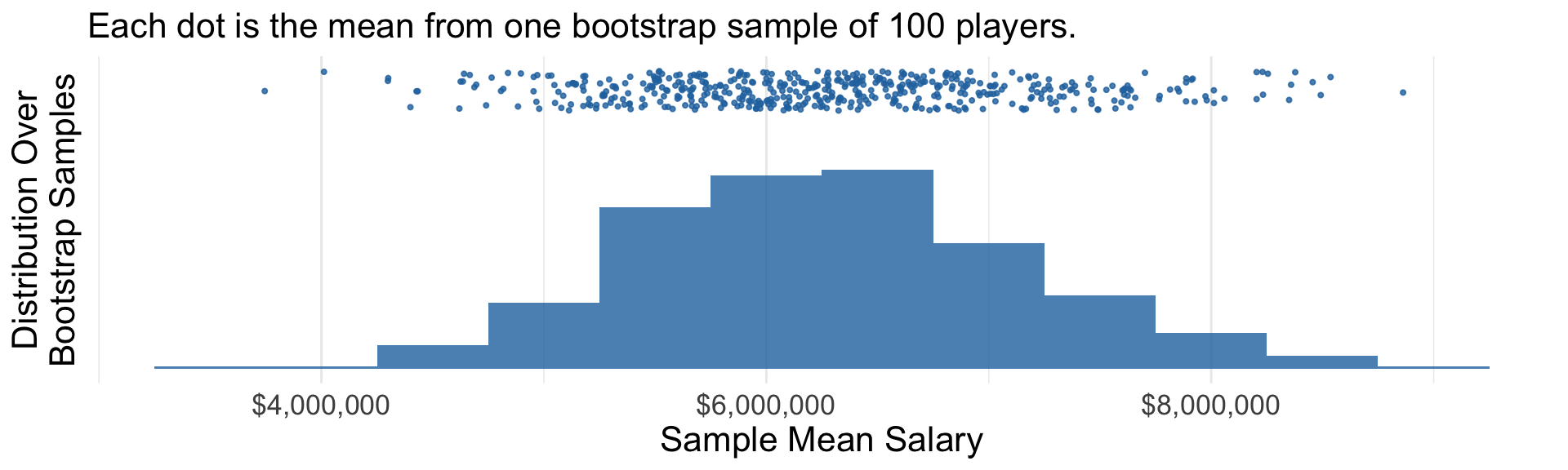
Bootstrap results: Summary statistics
Bootstrap estimate of the standard error.
Middle 95% of bootstrap estimates
Confidence interval
An interval from \(\text{lower}(\text{sample})\) to \(\text{upper}(\text{sample})\) with the property: across repeated samples, 95% of intervals constructed this way would contain the population parameter.
Confidence interval: Example
Middle 95% of bootstrap estimates is a confidence interval.
- The true population mean salary is $4,965,481
- Our sample mean is $6,254,938
- Our confidence interval is:
Across repeated samples, 95% of intervals constructed this way will contain the population mean salary.
Recap
- Statistical concepts
- Coding concepts
Recap: Statistical concepts
Statistical concepts
- Sampling distribution
- Cannot be directly observed. We have one sample.
- Standard error
- Spread of the sampling distribution
- Confidence interval
- Covers truth in 95% of samples
- Bootstrap
- Method of constructing the CI with one sample
Recap: Coding concepts
- Writing a custom function (R4DS Ch 25)
- Writing a for loop (R4DS Ch 27.5)