Conditional exchangeability

This topic is covered Feb 4. Here are slides.

Conditional exchangeability is an assumption that exchangeability holds within population subgroups. This assumption holds by design in a conditionally randomized experiment (discussed on this page), and may hold under certain causal beliefs in observational settings where the treatment is not randomized (next page).

A conditionally randomized experiment

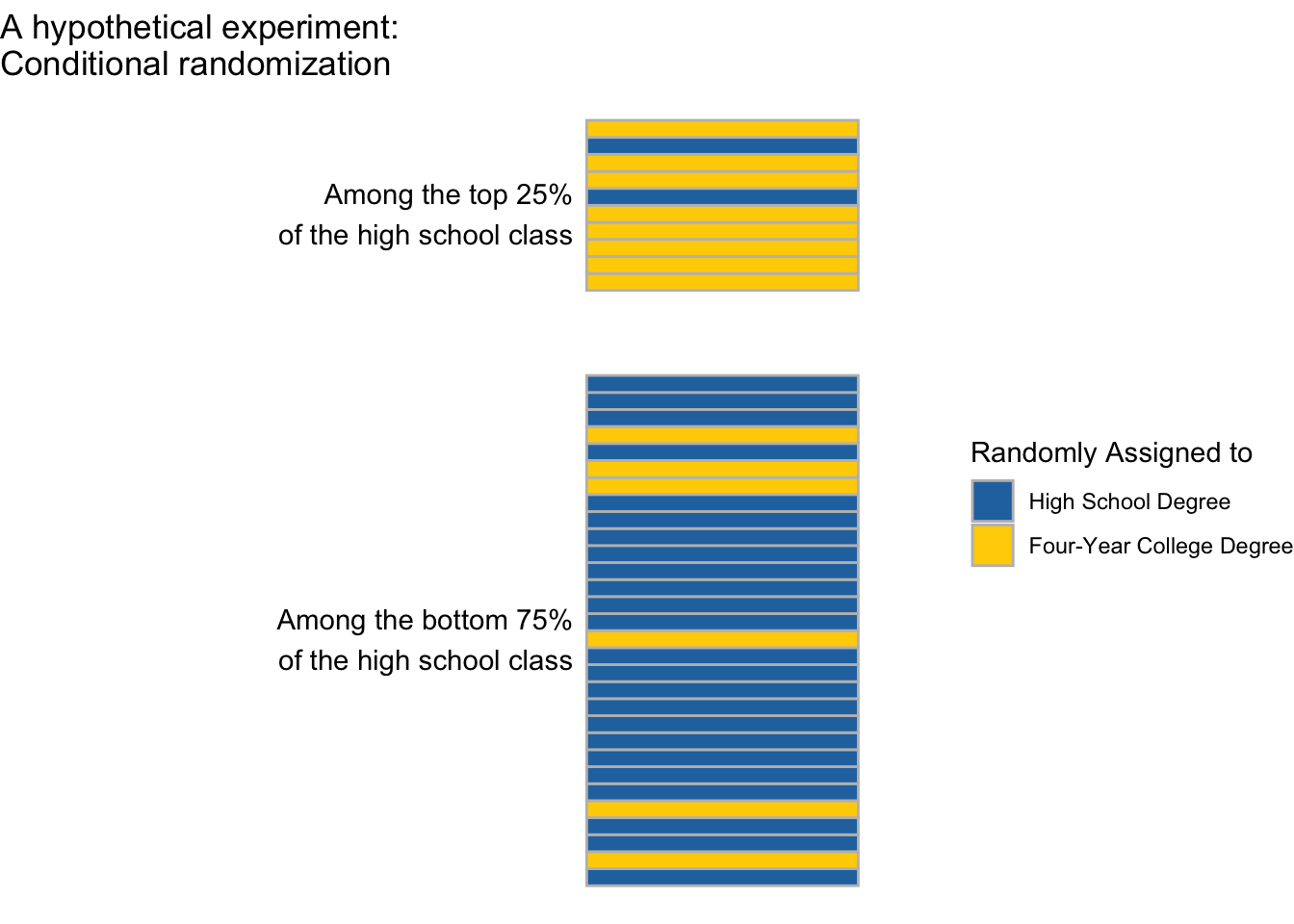
Suppose we were to carry out an experiment on a simple random sample of U.S. high school students. Among those performing in the top 25% of their high school class, we randomize 80% to attain a four-year college degree. Among those performing in the bottom 75% of their high school class, we randomize 20% to attain a four-year college degree. We are interested in effects on employment at age 40 (\(Y\)).

This experiment is conditionally randomized because the probability of treatment (four-year degree) is different among the higher- and lower-performing high school students.

Conditionally randomized experiment. An experiment in which the probability of treatment assignment depends on the values of pre-treatment covariates. \(\text{P}(A = 1\mid\vec{X} = \vec{x})\) depends on the value \(\vec{x}\).

Conditional exchangeability

In a conditionally randomized experiment, exchangeability is not likely to hold. People who are treated (assigned to a four-year degree) are more likely to have come from the top 25% of their high school class. They might be especially hard-working people. The treated and untreated might have had different employment at age 40 even if none of them had been treated.

Even though exchangeability does not hold marginally (across everyone), in a conditionally randomized experiment exchangeability does hold within subgroups. If we focus on those in the top 25% of the class, the 90% who are assigned to finish college are a simple random sample of the entire higher-performing subgroup. If we focus on those in the bottom 75% of the class, the 10% who are assigned to finish college are a simple random sample of the entire lower-performing subgroup.

Formally, conditional exchangeability takes the exchangeability assumption (\(\{Y^0,Y^1\}\unicode{x2AEB}A\)) and adds a conditioning bar \(\mid\vec{X}\), meaning that this assumption holds within subgroups defined by one or more pre-treatment variables \(\vec{X}\).

Conditional exchangeability. The assumption that potential outcomes \(\{Y^0,Y^1\}\) are independent of treatment \(A\) among subpopulations that are identical along a set of pre-treatment covariates \(\vec{X}\). Formally, \(\{Y^0,Y^1\} \unicode{x2AEB} A \mid \vec{X}\).

Conditional exchangeability holds by design in conditionally randomized experiments: the probability of treatment assignment differs across subgroups, but within each subgroup we have a simple randomized experiment where each unit has an equal probability of being treated.

Conditional average treatment effects

In our conditionally randomized experiment, we could identify conditional average treatment effects: the average effects of college on employment at age 40 (1) among those in the top 25% of their high school class, and the and (2) among those in the bottom 75% of their high school class.

Conditional average treatment effect (CATE). The average causal effect within a population subgroup, \(\tau(x) = \text{E}\left(Y^1\mid\vec{X} = \vec{x}\right) - \text{E}\left(Y^0\mid \vec{X} = \vec{x}\right)\).

Once we assume conditional exchangeability and consistency, CATEs are causally identified by working within a subgroup defined by \(\vec{X} = \vec{x}\) and taking the difference in means across subgroups of units assigned to treatment and control.

\[ \begin{aligned} &\text{E}\left(Y^1\mid\vec{X} = \vec{x}\right) - \text{E}\left(Y^0\mid\vec{X} = \vec{x}\right)\\ &= \text{E}\left(Y\mid\vec{X} = \vec{x}, A = 1\right) - \text{E}\left(Y\mid\vec{X} = \vec{x}, A = 0\right) \end{aligned} \]

In our concrete example, this means that we could first focus on the subgroup for whom \(\vec{X} = (\text{Top 25\% of high school class})\). Within this subgroup, we can compare employment at age 40 among those randomized to a 4-year college degree to employment at age 40 among those randomized to finish education after high school. This mean difference identifies the CATE: the average causal effect of college among those in the top 25% of their high school class.

Likewise, our experiment would also identify the CATE among those in the bottom 75% of their high school class.

Effect heterogeneity

There are often good reasons to expect the Conditional Average Treatment Effect (CATE) to differ across subpopulations. In our example, suppose that those from the top 25% of the high school class are very creative and hard-working, and would find ways to be employed at age 40 regardless of whether they finished college. The average causal effect of college on employment in this subgroup might be small. Meanwhile, the average causal effect of college on employment might be quite large among those from the bottom 75% of their high school class. This would be an example of effect heterogeneity,

Effect heterogeneity. Differences in Conditional Average Treatment Effects (CATEs) across subpopulations. \(\tau(\vec{x})\neq\tau(\vec{x}')\).

An advantage of analyzing randomized experiments conditionally (within subgroups) is that one can search for effect heterogeneity.